Fuzzy Finder on an Array Solution in Java
3 Ways to Rotate an Array
There's nothing easy about this algorithm

One of the most commonly found algorithms is the Rotate Array problem:
Given an array, rotate the array to the right by k steps, where k is non-negative. Try to come up as many solutions as you can — there are at least three different ways to solve this problem. Could you do it in place with O(1) extra space?
For example, if you were given the array [1, 2, 3, 4, 5] , and told to rotate it 2 steps to the right, the output should be [4, 5, 1, 2, 3]. After one rotation right, the array would be [5, 1, 2, 3, 4], so that after two rotations right, the array becomes [4, 5, 1, 2, 3].
On Leetcode, this problem is labeled "easy" — how they determine the difficulty level, I'm not sure. However, I think this problem is by no means easy. There are many ways to solve this problem, which is partly why I like it, and I think each solution is complicated in its own way.
In this article, I'll walk through three different ways to approach and solve this problem:
- Popping and unshifting the elements in the array.
- Creating a new array where the elements start out shifted.
- Reversing different sections of the array.
Approach #1: Popping and Unshifting
When working with arrays, a few methods come up all the time. One these is .pop(), which "removes the last element from an array and returns that element" (read more about .pop() here). For example:
const arr = [1, 2, 3]
arr.pop() // would return 3
console.log(arr) // would print [1, 2] Another common method used on arrays is .unshift(). This method "adds one or more elements to the beginning of an array and returns the new length of the array" (`read more about .unshift() here). For example:
const arr = [2, 3]
arr.unshift(1) // would return 3, the new length of the array
console.log(arr) // would print [1, 2, 3] Rotating an array right can also be thought of as moving the elements from the back of the array to the front of the array. In this problem, we want to move elements from the back of the array to the front, doing so k times. In a for loop, which will run k times, we can pop the last number off the back of the array, and unshift that number to the front of the array.
For example, let's say we were given the array nums = [1, 2, 3, 4, 5] and k = 2, so we should rotate the array twice. Using pop and unshift, we'd start by popping off the last element, 5, which would make nums = [1, 2, 3, 4]. Then, we unshift 5, putting it at the front of the array, so that nums = [5, 1, 2, 3, 4].
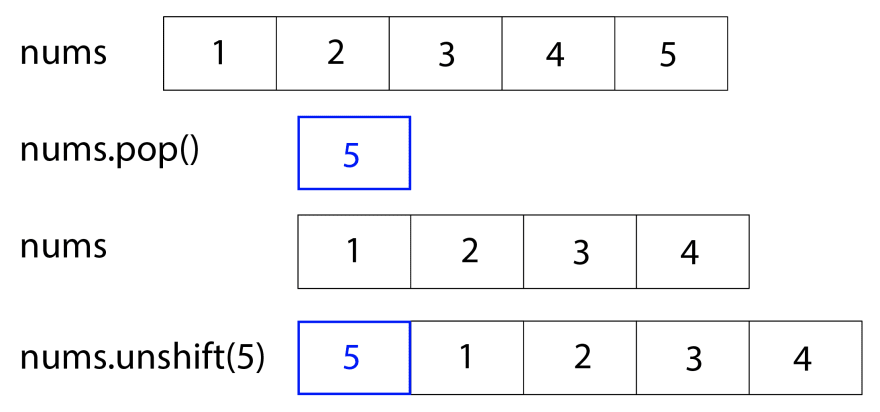
We repeat this cycle once more, popping off the 4, making nums = [5, 1, 2, 3], and then unshifting 4, giving us the final answer of nums = [4, 5, 1, 2, 3].
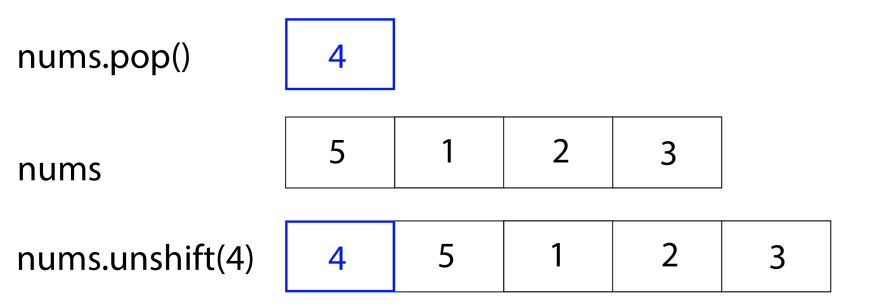
Coding the first approach
Before we start coding this solution, there's one more thing to note about this problem. Let's say that the given array was [1, 2], and we were told to rotate it to the right seven times. The array is less than seven elements long, so rotating it seven times would be a lot of unnecessary work. So, before we do anything, both in this solution and in the other approaches, we should modify k using modulo (%).
The modulo operator returns the remainder after dividing one number by another. For example, 10%3 would return 1, because 10/3 has a remainder of 1. Similarly, in this problem, we want to set k equal to k % nums.length. Using the same example, if k = 7, and nums = [1, 2], then k = k % nums.length is the same as k = 7%2, or k = 1. So, the first line of this solution will be this:
We want to do .pop()and .unshift() as many times as k equals, so we make a for loop that repeats k times. Inside the for loop, we store the result of nums.pop() to a variable called back. Then, we unshift back, putting it at the start of the nums array.
Once the for loop stops executing, we return nums.
This first approach is done in linear time (O(n)) and constant space (O(1)).
Approach #2: Creating a New Array
In the second approach, we're creating a new array, where the elements have moved over k spaces. The idea here is that we can just iterate through the nums array, and move each element k spaces to the right of where it was.
What happens if the element is supposed to move to an index that's longer than the length of the nums array? In that case, you use the modulo operator, calculating the result of moving to the new distance % the length of the nums array. I think this is a particularly tricky part of this approach, so I'll use an example.
Let's say you're starting out with the array nums = [1, 2, 3] and a blank array arr. We're told k = 2, so the array will move over 2 spots to the right. We start out by moving the first element of the nums array, 1. 1 is at index 0 (i = 0), and we want to move it two spots over. In other words, we want its position in the arr array to be determined by i + k which is index 2.
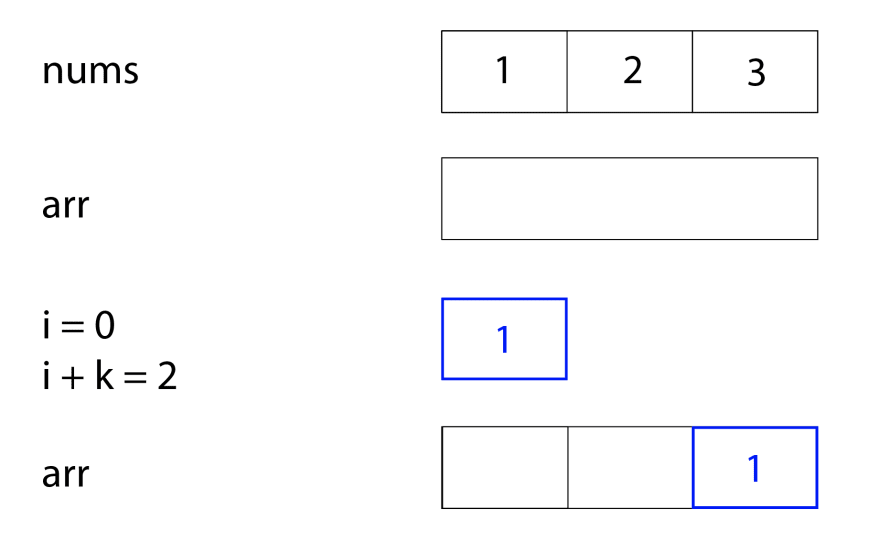
Now, we're on index one of the nums array, 2. We want to move it k steps to the right, but i + k is 3, and that would be longer than the length of the nums array. So, to find the new spot for 2, we should do (i + k) % nums.length, or 3%3, which is 0. So, we should move the element 2 to the index 0 in arr.
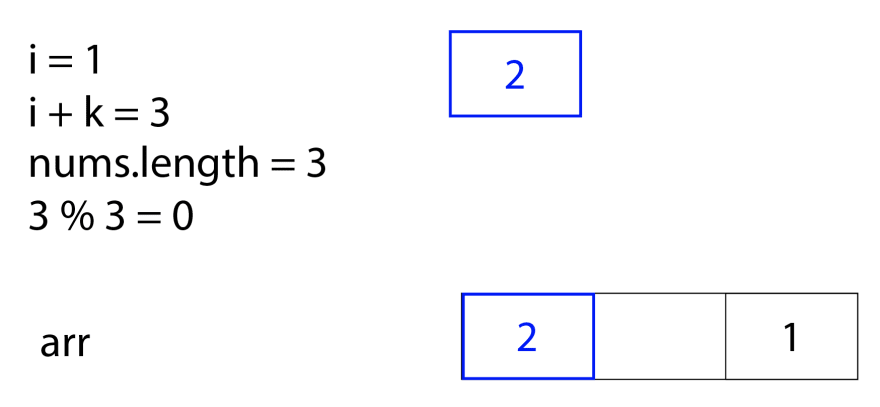
Finally, we're on the index two of the nums array, which is 3. We want to move it k steps to the right, and i + k is 4, which is longer than the length of the nums array. So, to find the new spot for 3, we should do (i + k) % nums.length, or 4%3, which is 1. So, we should move the element 3 to the index 1 in arr, giving us the final result of this problem.
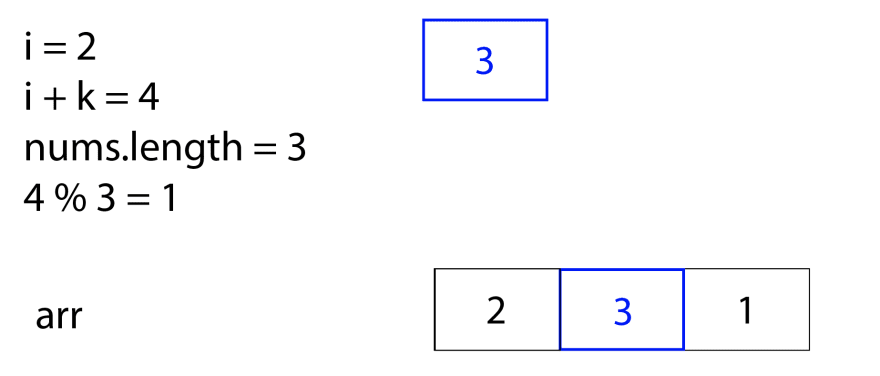
Coding the second approach
To start out this solution, we do the same modifications to k that we did in the first approach. We then initialize a new, empty array called arr.
Now, we use a for loop to go through every element in nums. At each index, we place that element in the new spot in arr. We can find that new spot by doing (i + k) % nums.length. So, we set arr[(i + k) % nums.length] equal to nums[i].
Now, arr will be the rotated array that we want. However, in this problem, we should be modifying the nums array, so we have to set each index in nums equal to the value at that index in arr. To do this, we set up another for loop. At each index, we'll set nums[i] equal to arr[i]. When the for loop ends, we can return nums.
This second approach is done in linear time (O(n)) and linear space (O(n)).
Approach #3: Reversing the Sections
In this third approach, we're going to be reversing parts of the nums. The first time, we reverse the entire array. The second time, we reverse the first k elements of the array. The third time, we reverse the final elements of the array, from k to the end.
The idea behind this approach is best be seen with an example. We start with the array [1, 2, 3, 4, 5], and we want to rotate it two steps. We start by rotating the entire array.

Now, we'll want to rotate the first k elements. Since k is 2, we'll rotate the elements at 0 and 1.

Finally, we'll rotate the last elements, from index k to the end. This gives us the final array that we want.

Coding the third approach
To code this solution, we'll write a function called reverse within the rotate function, and we'll call it three times. To start, however, we'll do the same modification to k that we did in the previous two approaches.
Then, we'll call the function reverse (which we'll write in a minute), and we'll call it three times. reverse() will take in the array, the index to start reversing, and the index to end reversing. So, the first call to reverse() will pass in nums, 0 (as the start index), and nums.length — 1 (as the end index). The second call to reverse() will pass in nums, 0 (as the start index), and k — 1 (as the end index). The third call to reverse() will pass in nums, k (as the start index), and nums.length — 1 (as the end index).
Now, we can write the function reverse, whose parameters will be nums, start, and end. In this function, we switch the values at the start and end index, and move start and end toward the center. We keep doing this as long as start is less than end.
So, we write a while loop, that will keep going as long as start is less than end. Inside the loop, we keep a temporary variable that stores the value of the nums array at the start index. Then, we set the value at the start index equal to the value at the end index and the value at the end index equal to the temporary variable. We move start toward the middle by incrementing it and we move the end toward the middle by decrementing it. Finally, when the while loop has executed, well return nums to the rotate function.
Once each reverse() function has executed, the final thing is to return nums:
This solution is done in linear time (O(n)) and constant space (O(1)).
Let me know in the comments if you have any questions or ideas for other ways to solve this!
Fuzzy Finder on an Array Solution in Java
Source: https://betterprogramming.pub/3-ways-to-rotate-an-array-2a45b39f7bec