What Phase Transitions Will Occur at 0ã‚â°c When the Pressure Is Dropped From 5 Atm to 0 Atm?
12.4: Phase Diagrams
- Page ID
- 24249
Learning Objectives
- To empathise the basics of a i-component phase diagram as a function of temperature and force per unit area in a closed system.
- To exist able to place the triple point, the critical point, and four regions: solid, liquid, gas, and a supercritical fluid.
The country exhibited by a given sample of thing depends on the identity, temperature, and pressure of the sample. A phase diagram is a graphic summary of the physical state of a substance equally a function of temperature and pressure level in a airtight system.
Introduction
A typical phase diagram consists of discrete regions that represent the unlike phases exhibited by a substance (Effigy \(\PageIndex{1}\)). Each region corresponds to the range of combinations of temperature and pressure level over which that phase is stable. The combination of high pressure and low temperature (upper left of Effigy \(\PageIndex{i}\)) corresponds to the solid phase, whereas the gas phase is favored at loftier temperature and low pressure (lower right). The combination of loftier temperature and loftier pressure (upper right) corresponds to a supercritical fluid.
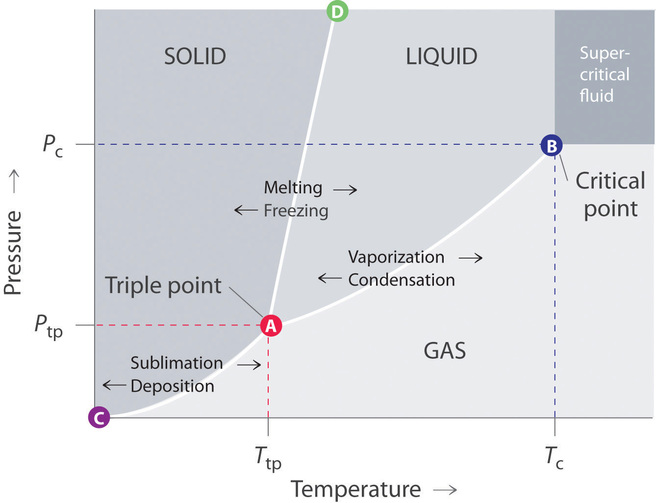
The solid phase is favored at depression temperature and high pressure; the gas phase is favored at high temperature and low pressure.
The lines in a phase diagram correspond to the combinations of temperature and pressure at which two phases can coexist in equilibrium. In Effigy \(\PageIndex{1}\), the line that connects points A and D separates the solid and liquid phases and shows how the melting point of a solid varies with pressure. The solid and liquid phases are in equilibrium all along this line; crossing the line horizontally corresponds to melting or freezing. The line that connects points A and B is the vapor pressure curve of the liquid, which we discussed in Section xi.5. It ends at the disquisitional point, beyond which the substance exists as a supercritical fluid. The line that connects points A and C is the vapor pressure curve of the solid phase. Along this line, the solid is in equilibrium with the vapor stage through sublimation and degradation. Finally, point A, where the solid/liquid, liquid/gas, and solid/gas lines intersect, is the triple point; it is the only combination of temperature and pressure at which all three phases (solid, liquid, and gas) are in equilibrium and tin can therefore be simultaneously. Considering no more than 3 phases tin always coexist, a phase diagram can never take more than three lines intersecting at a unmarried point.
Remember that a phase diagram, such as the one in Effigy \(\PageIndex{1}\), is for a unmarried pure substance in a airtight organisation, not for a liquid in an open beaker in contact with air at i atm force per unit area. In practise, however, the conclusions reached about the behavior of a substance in a closed system can ordinarily exist extrapolated to an open system without a bang-up deal of error.
The Phase Diagram of Water
Figure \(\PageIndex{2}\) shows the phase diagram of water and illustrates that the triple point of water occurs at 0.01°C and 0.00604 atm (four.59 mmHg). Far more reproducible than the melting point of ice, which depends on the corporeality of dissolved air and the atmospheric pressure, the triple point (273.16 Thousand) is used to define the absolute (Kelvin) temperature scale. The triple point besides represents the lowest pressure at which a liquid phase tin can exist in equilibrium with the solid or vapor. At pressures less than 0.00604 atm, therefore, ice does non melt to a liquid equally the temperature increases; the solid sublimes directly to water vapor. Sublimation of water at low temperature and pressure can be used to "freeze-dry out" foods and beverages. The food or beverage is start cooled to subzero temperatures and placed in a container in which the pressure level is maintained beneath 0.00604 atm. Then, as the temperature is increased, the water sublimes, leaving the dehydrated food (such as that used by backpackers or astronauts) or the powdered beverage (every bit with freeze-stale coffee).

The phase diagram for water illustrated in Figure \(\PageIndex{2b}\) shows the boundary between water ice and water on an expanded scale. The melting bend of water ice slopes up and slightly to the left rather than up and to the right every bit in Figure \(\PageIndex{1}\); that is, the melting point of ice decreases with increasing pressure; at 100 MPa (987 atm), ice melts at −ix°C. Water behaves this way because it is one of the few known substances for which the crystalline solid is less dense than the liquid (others include antimony and bismuth). Increasing the pressure of ice that is in equilibrium with water at 0°C and 1 atm tends to push some of the molecules closer together, thus decreasing the volume of the sample. The subtract in book (and corresponding increment in density) is smaller for a solid or a liquid than for a gas, simply it is sufficient to melt some of the water ice.
In Figure \(\PageIndex{2b}\) point A is located at P = 1 atm and T = −i.0°C, within the solid (ice) region of the stage diagram. As the pressure increases to 150 atm while the temperature remains the same, the line from point A crosses the water ice/water boundary to point B, which lies in the liquid water region. Consequently, applying a pressure of 150 atm will melt ice at −1.0°C. We take already indicated that the pressure dependence of the melting point of water is of vital importance. If the solid/liquid boundary in the phase diagram of water were to slant upward and to the right rather than to the left, ice would be denser than water, ice cubes would sink, water pipes would non burst when they freeze, and antifreeze would exist unnecessary in automobile engines.
Water ice Skating: An Incorrect Hypothesis of Phase Transitions
Until recently, many textbooks described ice skating every bit being possible considering the pressure level generated by the skater'southward blade is high enough to melt the water ice under the blade, thereby creating a lubricating layer of liquid water that enables the blade to slide across the ice. Although this explanation is intuitively satisfying, it is wrong, as nosotros can show past a elementary calculation.

Remember that pressure (P) is the force (F) practical per unit of measurement area (A):
\[P=\dfrac{F}{A} \nonumber\]
To calculate the pressure an ice skater exerts on the ice, we demand to calculate simply the force exerted and the area of the skate blade. If we presume a 75.0 kg (165 lb) skater, then the force exerted past the skater on the water ice due to gravity is
\[ F = mg \nonumber\]
where yard is the mass and m is the acceleration due to World's gravity (9.81 m/south2). Thus the force is
\[F = (75.0\; kg)(9.81\; m/s^2) = 736\; (kg•m)/s^2 = 736 N \nonumber\]
If we assume that the skate blades are two.0 mm wide and 25 cm long, then the expanse of the lesser of each blade is
\[ A = (2.0 \times ten^{−3}\; m)(25 \times x^{−2}\; thou) = 5.0 \times 10^{−4} m^ii \nonumber\]
If the skater is gliding on one human foot, the pressure exerted on the ice is
\[ P= \dfrac{736\;North}{5.0 \times 10^{-4} \; m^2} = 1.five \times ten^half dozen \; N/m^2 = i.5 \times 10^vi\; Pa =15 \; atm \nonumber\]
The pressure is much lower than the pressure needed to decrease the melting indicate of water ice by fifty-fifty i°C, and feel indicates that it is possible to skate even when the temperature is well below freezing. Thus pressure-induced melting of the ice cannot explain the low friction that enables skaters (and hockey pucks) to glide. Recent research indicates that the surface of ice, where the ordered assortment of water molecules meets the air, consists of one or more layers of almost liquid water. These layers, together with melting induced by friction as a skater pushes forward, appear to account for both the ease with which a skater glides and the fact that skating becomes more difficult below nearly −7°C, when the number of lubricating surface h2o layers decreases.
Example \(\PageIndex{1}\): Water
Referring to the phase diagram of water in Figure \(\PageIndex{ii}\):
- predict the physical form of a sample of water at 400°C and 150 atm.
- describe the changes that occur as the sample in part (a) is slowly immune to cool to −50°C at a constant pressure of 150 atm.
Given: phase diagram, temperature, and pressure
Asked for: physical form and physical changes
Strategy:
- Place the region of the phase diagram corresponding to the initial weather condition and identify the stage that exists in this region.
- Depict a line corresponding to the given pressure. Motion forth that line in the appropriate direction (in this example cooling) and describe the stage changes.
Solution:
- A Locate the starting signal on the phase diagram in part (a) in Effigy \(\PageIndex{two}\). The initial conditions correspond to indicate A, which lies in the region of the phase diagram representing h2o vapor. Thus water at T = 400°C and P = 150 atm is a gas.
- B Cooling the sample at constant pressure corresponds to moving left along the horizontal line in function (a) in Figure \(\PageIndex{2}\). At about 340°C (point B), we cross the vapor pressure bend, at which indicate water vapor will begin to condense and the sample will consist of a mixture of vapor and liquid. When all of the vapor has condensed, the temperature drops further, and we enter the region respective to liquid water (indicated by point C). Further cooling brings us to the melting curve, the line that separates the liquid and solid phases at a lilliputian below 0°C (point D), at which point the sample volition consist of a mixture of liquid and solid water (water ice). When all of the water has frozen, cooling the sample to −50°C takes u.s. along the horizontal line to point Due east, which lies within the region corresponding to solid water. At P = 150 atm and T = −50°C, therefore, the sample is solid ice.
Exercise \(\PageIndex{two}\)
Referring to the phase diagram of water in Figure \(\PageIndex{2}\), predict the concrete form of a sample of h2o at −0.0050°C as the pressure is gradually increased from ane.0 mmHg to 218 atm.
- Reply
-
The sample is initially a gas, condenses to a solid as the pressure increases, and and so melts when the force per unit area is increased farther to requite a liquid.
The Stage Diagram of Carbon Dioxide
In contrast to the phase diagram of water, the phase diagram of CO2 (Figure \(\PageIndex{3}\)) has a more than typical melting curve, sloping up and to the right. The triple point is −56.6°C and 5.11 atm, which means that liquid CO2 cannot exist at pressures lower than five.11 atm. At 1 atm, therefore, solid CO2 sublimes directly to the vapor while maintaining a temperature of −78.5°C, the normal sublimation temperature. Solid COii is generally known as dry water ice because it is a common cold solid with no liquid phase observed when information technology is warmed.

Besides observe the critical indicate at 30.98°C and 72.79 atm. Supercritical carbon dioxide is emerging every bit a natural refrigerant, making information technology a low carbon (and thus a more environmentally friendly) solution for domestic estrus pumps.

The Disquisitional Point
As the stage diagrams above demonstrate, a combination of loftier force per unit area and low temperature allows gases to exist liquefied. As nosotros increase the temperature of a gas, liquefaction becomes more and more than difficult because higher and higher pressures are required to overcome the increased kinetic free energy of the molecules. In fact, for every substance, in that location is some temperature above which the gas can no longer be liquefied, regardless of pressure. This temperature is the critical temperature (T c), the highest temperature at which a substance can exist equally a liquid. Above the critical temperature, the molecules have too much kinetic energy for the intermolecular bonny forces to agree them together in a divide liquid phase. Instead, the substance forms a single phase that completely occupies the book of the container. Substances with stiff intermolecular forces tend to form a liquid phase over a very big temperature range and therefore have high critical temperatures. Conversely, substances with weak intermolecular interactions take relatively low critical temperatures. Each substance likewise has a disquisitional pressure (P c), the minimum force per unit area needed to liquefy it at the critical temperature. The combination of critical temperature and critical pressure is called the disquisitional point. The disquisitional temperatures and pressures of several mutual substances are listed in Figure \(\PageIndex{1}\).
| Substance | Tc (°C) | Pc (atm) |
|---|---|---|
| NH3 | 132.4 | 113.5 |
| CO2 | 31.0 | 73.8 |
| CH3CHtwoOH (ethanol) | 240.9 | 61.iv |
| He | −267.96 | ii.27 |
| Hg | 1477 | 1587 |
| CHfour | −82.6 | 46.0 |
| Northward2 | −146.9 | 33.9 |
| HtwoO | 374.0 | 217.7 |
High-boiling-point, nonvolatile liquids have high disquisitional temperatures and vice versa.
Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map:_General_Chemistry_%28Petrucci_et_al.%29/12:_Intermolecular_Forces:_Liquids_And_Solids/12.4:_Phase_Diagrams